FitNets: Hints for Thin Deep Nets

Abstract

일반적으로 Network architecture에서, network의 depth가 깊어질수록 성능이 더 좋아지지만, non-linear activation을 더 많이 거치게 되므로 gradient-based training이 어렵게 된다.

최근(2015년 기준) 제안되고 있는 knowledge distillation 방법들은 크기가 작고 실행이 빠른 모델(fast-to-execute)을 목표로 하고 있다. 그리고 이를 만족하는 student model이 크기가 크거나 모델들의 앙상블로 구성된 teacher model의 soft output을 근사시킬수 있다는 것이 증명되었다.

이 논문에서는 이 아이디어를 확장시켜서 student model이 teacher model에 비해 네트워크 구조가 깊고 얇은 (deeper and thinner) 것으로 학습시키고자 한다. 또한 training 과정에서 teacher의 output들(soft label, hard label)뿐만 아니라 teacher이 학습한 intermediate representation이 활용되어 student에게 “hint”로 주어진다. student의 intermediate layer가 teacher의 intermediate layer보다 일반적으로 크기가 작을 것이기 때문에, 추가적인 파라미터를 이용해 student의 hidden layer를 mapping 하여 teacher의 hidden layer를 예측하게 한다. 이를 통해 깊은 student 모델을 학습시켜 더 나은 generalization을 갖거나 빠른 실행 속도를 가능하게 한다. 두 trade-off 사이를 조절하기 위해 student의 파라미터 용량을 조절할 수 있다. 예를 들어, CIFAR-10 에서 논문이 제시한 deep student network는 10.4배 적은 파라미터 수를 가지고도 더 큰 SOTA 모델의 성능을 능가한다.

Introduction

많은 네트워크들이 컴퓨터 비전 분야에서 SOTA 성능을 보여주고 있지만, 가장 뛰어난 성능을 보이는 것들은 대부분 깊고 넓은 구조를 갖고 있다. 이 때문에 inference time이 길고, 파라미터 수가 많아 큰 메모리 용량을 차지한다.

위 두가지 문제들을 해결하기 위해서 모델 압축과 관련해 몇몇 연구가 진행되어왔다. (복잡하고 크기가 큰) 앙상블 모델의 출력을 라벨로 받아 학습시켜 앙상블을 흉내내는 방향으로 네트워크를 학습시키기도 했으며(Bucila et al, 2006), 같은 방법으로 얇고 넓은 구조의 네트워크를 학습시키기도 했다(Ba & Caruana, 2014).

한편, 힌튼이 모델 압축 프레임워크로 제시한 Knowledge Distillation(2014)는 깊은 네트워크를 더 쉽게 학습시킬 수 있도록 하는 student-teacher paradigm을 제시하였다. student-teacher 개념을 미리 간단히 설명하자면, student는 teacher(모델 앙상블)과 비슷한 depth를 가지는 하나의 압축된 모델이다. 이때 student는 teacher output의 soft label(소프트맥스 값)을 hard label(진짜 라벨)과 함께 이용하여 학습시킨다.

지금까지 살펴본 모든 논문들에서, 모델 압축 연구들은 비슷한 depth & width 혹은 shallow & wider 모델들을 사용했으며, depth를 키워서 얻을 수 있는 이득을 취하지 못했다. 네트워크에서 Depth가 깊어질수록 피처들이 반복해서 사용되고, 높은 층의 레이어에서 더 abstract하고 invariant한 representation이 나타나기 때문에 representation learning 관점에서 네트워크의 Depth는 중요하다.

하지만 depth가 깊은 네트워크는 activation이 여러번 연속적으로 구성되어있기 때문에 non-convex, non-linear 하여 학습시키기가 어려웠으며, 이를 해결하기 위한 많은 연구들이 있었다. 먼저 pre-training 방법의 일환으로서 AutoEncoder와 유사한 greedy-layerwise training을 살펴본다.

---

AutoEncoder의 경우 hidden layer가 하나이고, unsupervised learning으로 입력 데이터 x 를 feature로 학습시키고, 이를 다시 x에 근접한 값이 나오도록 출력을 학습시킨다. 학습을 마치고 최종단을 제거하면, hidden layer는 입력데이터의 특징을 잘 추출할 수 있게 된다.

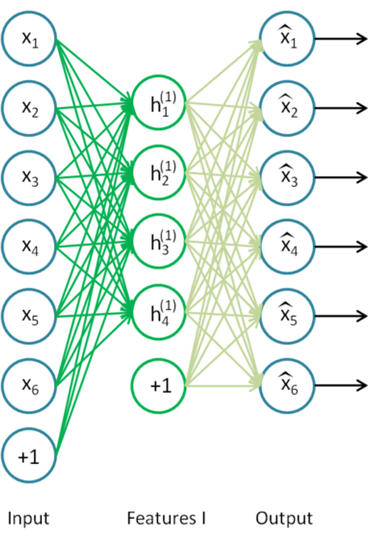
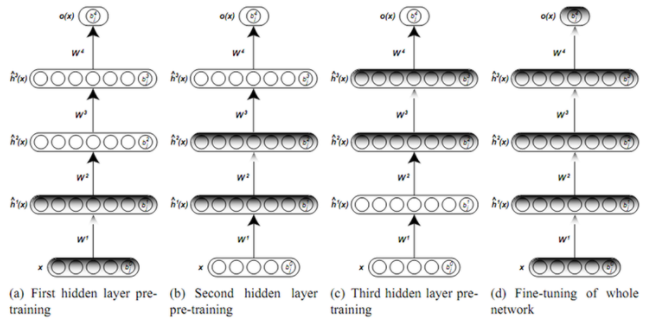
Greedy layer-wise training에서는 각 단계별로 AutoEncoder를 학습시키는 것으로 생각할 수 있다. (a)에서 first hidden layer만 존재하는 것으로 가정하고 뒤의 layer들은 없다고 생각한다면 하나의 AutoEncoder를 학습시키는 것과 같게 된다. (b)에서는 first 와 third의 파라미터를 고정시키고, second layer만 있는 것으로 학습시킨다. 이때는 앞 단계에서 학습한 first hidden layer의 output을 input으로 학습시키는 것으로 생각할 수 있으며 마찬가지로 AutoEncoder 개념으로 생각할 수 있다. 이런 방식으로 마지막 레이어까지 layer별로 greedy하게 학습을 시키게 된다면, 여러개의 hidden layer들이 있어도 학습이 가능해지게 된다.

---

이와 비슷한 방법들로, semi supervised embedding을 이용하여 intermediate layer들에 guidance를 주는 시도가 있었으며(Weston, 2008), DBM의 최적화를 위해 다른 모델의 매 두번째 layer들의 activation을 가져와 unsupervised learning의 방법으로 학습하려는 시도가 있었고(Cho, 2012), 더 근래에는 intermediate layer들에 supervision을 추가해서 학습을 돕는 방법이 제안되었다(Chen-Yu, 2014). 여기서 supervision은 intermediate hidden layer위에 softmax layer가 포함된 multi-layer를 올리는 것으로서 hidden layer가 각 라벨들에 대한 분별 능력을 갖추도록 했다. 다른 접근으로는, Curriculum Learning 방법으로서 (Bengio, 2009) 사람이 쉬운 것부터 시작해서 점차 어려운 것을 배우는 것처럼, 최적화 문제를 training data의 distribution을 조절하는 것으로 해결했다. 네트워크가 이미 학습한 정보에 따라 점점 더 어려운 데이터(노이즈가 많거나, 가우시안 분포의 boundary에서 margin 거리가 먼 데이터)를 학습시키는 방법을 이용했다. 이를 통해 더 빠른 convergence를 가능하게 하고, highly non-convex function에서 better local minima를 찾게 해주었다.

이 논문에서 집중하고자 하는 것은, 모델 압축 문제를 depth를 이용하여 해결하는 것이다. 이에 wide and relatively shallow한 teacher 모델을 압축시키는 thin and deep network, FitNet이라는 새로운 네트워크를 제안한다. 논문의 아이디어는 Hinton이 발표한 Knowledge Distillation에 기반하고 있으며 이를 thinner and deeper한 student 모델로 확장시킨다. Teacher 모델의 hidden layer들을 intermediate-level hint로서 student의 학습을 돕는다. 이때 teacher의 intermediate representation과 student 모델(FitNet)의 intermediate representation이 유사하도록 학습하게 된다. Hint는 네트워크 구조가 thinner and deeper 할 수 있도록 해준다. 실험 결과를 통해 FitNet의 deep 특성은 더 나은 generalization을 보여주면서 동시에 thin한 특성은 연산량을 줄여준다. MNIST, CIFAR-10, CIFAR-100, SVHN, AFLW 등의 데이터셋 벤치마크를 통해 훨씬 적은 parameter와 계산들을 사용하면서도 teacher의 성능과 엇비슷하거나 outperform하는 결과를 보여준다.

Method

Review of Knowledge Distillation

이 논문은 KD에 뿌리를 두고 있기 때문에, 관련 내용을 리뷰하도록 하는 것이 좋겠다. Teacher Network에서 a_t가 소프트맥스를 거치기 전 출력, 소프트맥스 activation을 거친 출력값을 P_t = softmax(a_t)라고 할 때, 마찬가지로 Student에서는 P_s = softmax(a_s)라고 표현하도록 하겠다. 이때 P_t가 true label의 one hot coding 처럼 작용할 수 있으므로(예를 들어 확률값이 0.01, 0.02, 0.97일 경우 소프트맥스값과 라벨 차이가 큰 의미가 없다.) relaxation term r >1 을 도입해서, 출력을 soften하는 효과를 주어 학습시킬 때 더 많은 정보를 주게 한다. 이에 대한 설명을 쉬운 예로 생각해보자.

차 소프트맥스 출력값 0.1, 비행기 소프트맥스 출력값 0.8 이고 정답이 비행기라고 가정. 여기서 차 출력값이 0이 아니라 0.1이라는것은 (예를 들어) 차 바퀴의 모양이 비행기의 바퀴의 모양과 비슷하다는 것과 같은 부분적인 정보를 담고 있을 수 있다. 그러나 단지 라벨만 가지고 학습하면 이런 정보를 얻을 수 없으며, relaxation을 도입하지 않았을 경우 확률값이 너무 작기 때문에 반영이 되기 어렵다. 그래서 소프트맥스 전 아웃풋에 relaxation을 도입하면, 위 소프트맥스 출력값이 기존 0.1, 0.8 이었던것이 0.3, 0.6 정도로 바뀌어 차에 대한 정보도 일부분 받아들이는 학습이 가능하다.

다시 돌아가서 KD에서 정의하는 relaxation이 적용된 probability를 살펴보면 다음과 같다.

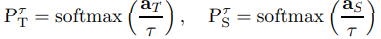
위 정의를 토대로 Student 는 다음 식에 따라 학습된다.

H는 cross entropy, 람다는 두 cross entropy값 사이를 조절하는 튜닝 파라미터이다. 람다값은 뒤에 나올 curriculum learning과 관련이 있다. 위 식에서 앞단은 전통적인 student와 라벨 사이의 CE이고, 뒷단은 teacher의 softened 출력으로부터 학습할 수 있도록 하는 부분이다.

Hint-Based Training

이 논문이 제시하는 FitNet이라는 Student의 학습을 위해서, “Hint”의 개념을 도입하게 된다. Hint는 Teacher의 hidden layer 출력으로서 Student의 학습을 ‘가이드’하는 것이다. 여기서 Teacher의 Hint layer로부터 가이드 되는 Student의 레이어를 Guided Layer라고 할 때, 우리는 guided layer가 hint layer의 output을 예측하도록 하는 것이 목표이다.

여기서 Hint는 하나의 regularize form으로 생각할 수 있는데, 이때 hint/guided layer를 deeper layer(입력층으로 부터 먼 layer)로 사용하게 된다면 student가 over-regularized 되므로 적절한 곳에 hint/guided layer를 설정해야 한다. 따라서 여기에서는 middle layer를 teacher의 hint, student의 guided layer로 설정한다고 한다.

한편, teacher network는 일반적으로 FitNet보다 넓은 구조로 되어 있을 것이므로, hint layer의 출력이 guided의 출력보다 더 많은 dimension을 갖고 있을 것이다. 따라서 regressor term을 도입하게 되는데, regressor 함수는 guided layer의 출력이 hint layer출력과 같은 사이즈를 갖도록 매칭시킨다.

FitNet의 파라미터들에 대한 학습에서는, 입력층부터 Guided layer까지의 layer parameter들과 regressor parameter을 함께 학습시킨다. loss 식은 다음과 같다.

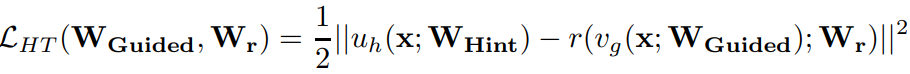
여기서 U_h, V_g는 teacher/student 각각의 hint/guided 까지의 deep nested function이며 r은 regressor 함수이다. 값의 비교를 위해서 U_h 와 r은 same non-linearity를 가져야 한다.(같은 activation을 준다는 말인 것 같다.)

한편 fully connected regressor를 사용한다면 파라미터 수는 Nh,1×Nh,2×Oh×Ng,1×Ng,2×Og 개로 엄청나게 많은 파라미터를 필요를 한다. 이 때문에 convolutional regressor를 도입하게 된다. Teacher hint의 spatial size를 Nh1 X Nh2, FitNet Guided의 spatial size를 Ng1 X Ng2 라고 할때, 커널 k1 X k2 를 만들어 Ng - k + 1 = Nh를 만족하게 한다. 쉽게 생각하면 Ng를 이미지라 생각했을 때 출력의 크기가 Nh가 되게 하는 커널k를 convolutional regressor로 채용한다는 것이다. 이렇게 했을 때 regressor의 파라미터 수는 k1 × k2 × Oh × Og 가 되어 훨씬 적어진다.

FitNet Stage-wise Training

학습 파이프라인을 설명한다. 먼저 기학습된 teacher network와 randomly initialized된 FitNet을 가지고 시작한다. FitNet의 Guided layer 위에 regressor를 올리고 다음 식에 대해 최적화한다. 식에서 주의해야할 것은 W_guided, W_hint는 각 층에만 해당하는 것이 아니라 시작부터 guided/hint 층 까지의 모든 파라미터(up to guided/hint)를 말하는 것이다.

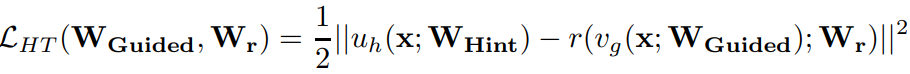
그 다음으로, Guided layer까지 pretrained된 것을 바탕으로, student network 전체를 다음 식에 대해서 최적화한다.

정리된 알고리즘 명세를 확인하면 쉽게 이해가 가능하다

Relation to Curriculum Learning

위 Introduction에서 Curriculum Learning 에 대한 설명을 약간 해보았는데, FitNet에서도 이 개념이 적용된다고 주장하고 있다. Curriculum Learning의 개념은 쉬운 example로부터 시작하여 점점 complex example을 학습하여 빠른 convergence와 generalization을 갖는 것이다. 기존 연구들은 “sim, FitNet에서는 KD loss의 파라미터였던 람다값의 decay를 통해 이를 실현한다.

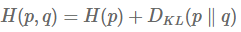
위 식에서 뒷단인 P_t 와 P_s 사이의 cross entropy는 P_t의 엔트로피와 P_t, P_s 사이의 KL divergence의 합으로 생각할 수 있다.또 confidence가 높다는 것은 결국 쉬운 example을 학습하는 것으로 생각할 수 있다. 따라서 학습 초기에 쉬운 example을 학습할 때는 람다값 $\lambda$ 을 높게 설정하여 학습 효과를 크게 주고, 학습이 진행되고 점점 어려운 example들을 학습하게 되면 $\lambda$ 값 또한 linear decay시켜 학습에 미치는 영향을 줄이게 한다.

Results

CIFAR-10 and CIFAR-100

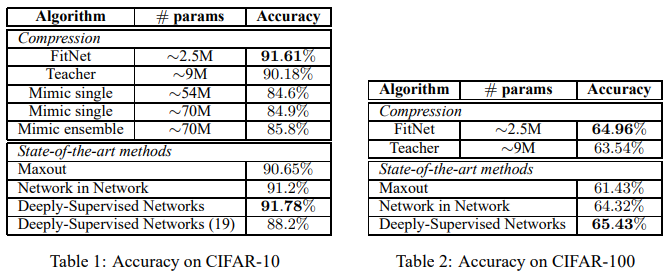
CIFAR-10 : 검증에 사용된 Teacher 모델은 maxout networks(Goodfellow, 2013)이며, FitNet은 17개 maxout convolutional layer와 maxout fc layer, softmax layer로 연결된 구조로서 Teacher의 1/3 정도의 파라미터 개수로 구성했다. Student의 11번째 layer는 Teacher의 2번쨰 layer를 mimic하도록 한다. (각각을 Hint, Guided로 설정한다). Student model이 상당히 적은 파라미터 개수로도 Teacher model을 outperform 하는 것을 확인할 수 있으며, 이는 모델의 depth가 더 좋은 representation을 갖는 것에 중요한 요소임을 알 수 있다. FitNet의 accuracy가 91.61로 다른 model compression 방법(Ba & Caruna, 2014)의 accuracy 85.8%과 비교하였을 때, 훨씬 적은 파라미터 수로도 더 좋은 성능을 보여준다. 뿐만 아니라, 당시의 SOTA와 비교하였을때도 뒤지지 않는 성능을 보여준다.

CIFAR-100:

CIFAR-10과 마찬가지로 적은 파라미터 수로 좋은 accuracy를 보여주고 있다. 다른 compression 모델과의 비교는 빠져있는데, 논문에서 따로 그 이유는 밝히지 않았다.

SVHN & MNIST

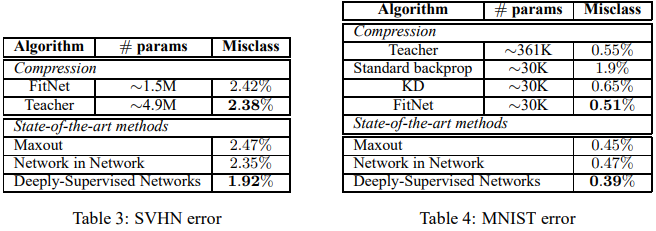
SVHN: google streetview 활용한 house number 32 X 32 컬러 이미지

Teacher를 maxout network, FitNet을 11 maxout conv layer, fc layer, softmax layer로 설정. Teacher 대비 32%의 파라미터 개수로 비슷한 성능 보여준다. 다른 SOTA method에 뒤지지 않음.

MNIST: 학습이 잘 되는지 sanity check 용도로 사용. Teacher는 동일하게 maxout network 사용하였으며 FitNet은 8%의 파라미터 개수로 Depth가 2배인 모델 사용. Hint의 유용성을 평가하기 위해 Standard backprop, KD, HT를 각각 사용했을 때의 결과들을 구했다. FitNet 을 softmax layer로부터 standard backprop했을 때 1.9 % misclassification을 보여주었고, 같은 네트워크에서 KD를 사용했을 때 0.65%의 misclass를 보여주어 teacher network의 유용성을 알 수 있다. 한편 Hint를 사용했을 때 0.51%로 줄어들어 더 좋은 성능을 냄을 알 수 있고, 결론적으로 12배 적은 파라미터 개수로 teacher보다 좋은 성능을 냄을 알 수 있다.

AFLW

AFLW: a real world face database, containing 25K annotated images.

Face recognition을 위해 positive sample을 25K 16 X 16 resize,

ImageNet으로부터 not containing face image 25K 16 X 16 resize.

Teacher: 3 ReLU conv layer and a sigmoid output layer

FitNet 1: 7 ReLU conv layer and a sigmoid output layer, 15times fewer multiplication

FitNet 2: 7 ReLU conv layer and a sigmoid output layer, 2.5times fewer multiplication

missclassification on the validation set:

Teacher: 4.21% (misclasss)

FitNet 1 with KD: 4.58 %,

FitNet 1 with HT: 2.55 %

FitNet 2 with KD: 1.95 %

FitNet 2 with HT: 1.85%

실험 결과는 다양한 네트워크 구조에 확대 적용 가능하며, 특히 깊은 네트워크를 사용했을 때 Hint를 사용함으로서 얻을 수 있는 성능 이익을 확인 가능하다.

Analysis of Empirical Results

논문에서 제안한 방법이 얼마나 효과적인지 검증하기 위해 standard backprop (라벨에 대한 cross entropy), KD, 그리고 HT(Hint based Training)의 방법으로 다양한 네트워크들을 학습시켜보았다. 실험은 CIFAR-10으로 하였다. 총 계산량을 정해놓고(computational budget) 그 주어진 계산량 안에서 conv layer의 채널 수 와 네트워크 depth만 변경시키면서 실험하였다. 이때 네트워크 구성은 3X3 conv, maxout, 2X2 max pooling의 블록들로 구성하는 것으로 정했다.

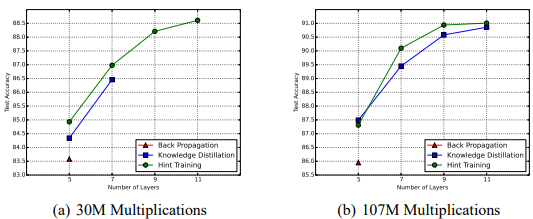
먼저, HT의 영향에 대해서 살펴본다. Computation budget을 각각 30M, 107M OPs 로 두었을때, 네트워크 레이어 수와 training 방법 (standard backprop, KD, HT)를 달리하여 실험하였다. 기본적으로 FitNet은 deep and small capacity이기 때문에, Standard Backprop 으로 학습이 잘 되지 않는다. KD를 사용했을 때 위에서 설명한 curriculum learning의 장점을 살려 한층 더 나은 optimization이 가능하지만 그림(a)를 보면 여전히 7 layers 에서 성능향상이 멈춰버리게 된다. 이에 비해 HT를 이용하면 11 layers까지 test accuracy가 증가하는 것을 볼 수 있다. HT와 KD의 단 하나의 차이는 parameter space의 initialize, 즉 아예 랜덤으로 시작할 것이지, 아니면 Teacher의 힌트를 받고 시작할 것인지이다. HT이 더 나은 initial position을 갖기 떄문에, optimization 관점에서 유리하다. 또한 test set에 대해 좋은 성능을 보여주는 것을 통해, HT가 KD보다 더 강한 regularizer로서 작용한다는 것을 알 수 있다. 마지막으로, 이 실험은 계산량을 고정시키고 layer의 수를 변경시켰을 때의 성능을 보여주면서 네트워크가 깊어질수록 더 나은 성능을 보여주는 것을 보여준다.

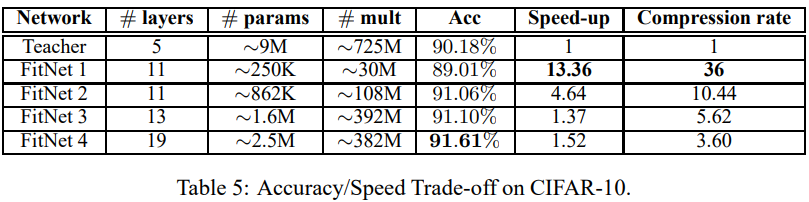
FitNet의 efficiency 측정을 위해, parameter compression과 GPU에서 inference time을 비교한 table이다. 모델의 performance(accuracy)와 efficiency(inference time) 사이의 trade-off 를 확인할 수 있었다. Compression rate는 이 trade off를 설명하는 단위로 생각할 수 있다. (성능 하락에 비해서 속도가 얼마나 빨라졌는지) FitNet은 상당히 빠른 inference 속도를 보여주며, 적은 파라미터 수로 teacher의 성능을 능가하고 있다.

Conclusion

논문이 제시한 새로운 framework FItNet은 기존의 wide and deep networks를 thin and deeper 모델로 압축시킨다. 이를 위해 intermediate-level hint를 도입하여 student의 guided layer가 teacher의 hidden layer(Hint layer)에 의해 학습 과정에서 도움을 받는다. hint를 도입함으로서 적은 수의 파라미터로 이루어진 매우 깊은 층의 네트워크도 학습할 수 있게 되었고, teacher보다 더 나은 generalization, inference speed를 가진 student model를 학습시킬 수 있었다.